In the previous post, I’ve made an overview of what it is to be an object, how it is different from properties, and I’ve taken a look inside it. What I haven’t considered is an intuitive difference between objects like my chair, my phone, or Matt Berninger and entities like number 7, an apple, Monday, sadness, the architecture of ancient Rome, the proposition “I like coffee”, and the direction that my pencil is pointing at right now. What are they? On one hand, they can act as subjects, and some of them can be quantified over and thought of. From another, most of them are out of spacetime and we can’t tell their exact location. Following this intuitive distinction alone, objects from the second group are called abstract, as an opposite to concrete objects from the first group. Here, I’ll set off different ways to draw a line between them.

The Way of Negation

This approach boils down to noting the traits that abstract objects lack, but concrete ones possess. Gottlob Frege seems to be the first one who has stated it explicitly and clearly. He said that abstract objects are non-mental and non-physical. This statement is the basis of an argument that draws the conclusion that abstract objects exist. In it, objects pre-considered to be abstract are taken and it’s proved that they can be neither mental nor physical. Typical examples of abstract objects are numbers, propositions, properties and relations, types, or kinds, of objects (as opposed to concrete items belonging to a certain kind, like the fruit lying in front of me right now is an apple, or in other words, belongs to an apple kind), and fictional objects like Sherlock Holmes.

A typical example of a mental entity is a thought. Our minds are the only place that any particular thought can exist in. More generally, mental objects are parts of someone’s mental state. When in doubt whether some object is mental or not, ask yourself a question: if the human mind didn’t exist, would this object still be there? If it would, then it’s not mental. Take some specific apple, for instance. If mankind suddenly perished in one moment so that nobody could ever think about it, this apple would still exist for some time.

Calling some object non-physical means that it has nothing to do with the laws of physics. It’s not made of physical stuff. Such objects are not something you can find and interact with in Nature. For instance, if you accept that there is an object representing red color, it is totally non-physical, in contrast to red apples, red hydrants, and red roses.

Let’s consider two examples illustrating an argument about the existence of abstract objects.

Numbers

Numbers are largely dismissed as being mental entities, and for good reason. First of all, there is an infinite amount of numbers, and hence, there is an infinite amount of numbers no one ever thought about. Second, if mankind died, the truth value of 7 > 3 would be hard to define (and if it would, it would be false), because no such things as 7 or 3 would exist. This seems unlikely because truths in mathematics don’t depend on whether we’re alive or not.

Numbers, as well as other mathematical objects, are not taken as physical entities either. Although Immanent Realism claims otherwise. In this view, numbers are properties of piles of concrete objects. From the mathematical perspective, those piles are sets that behave in accordance with the Set Theory. So, cardinal numbers of sets of physical objects are implied to bijectively correspond to natural numbers. And that’s where things get ambiguous. Let’s say there are two apples. Together, they form a set of two apples. But besides that set, there is a set of all the molecules that those apples consist of. And there is a set of a set of two apples. And a set containing an apple and a set containing another apple. In other words, there is an infinite amount of possible sets, with an infinite amount of possible cardinal numbers, and each of them is about the same physical stuff. But which set correctly describes number two? If you think it’s the one with just two apples as members, why? What makes this set so special? On these grounds, Immanent Realist’s views about numbers are largely discarded.

Finally, we have to deal with Nominalism, or, to be precise, with one of its branches called Fictionalism. It presents the biggest challenge to Platonism, at least on the matter of numbers. In a nutshell, fictionalism boils down to the rejection of abstract objects as such. Their main argument is that humans have no way to attain knowledge about them because those objects are non-physical, non-spatiotemporal, and causally inefficacious - in other words, abstract. This draws an unpalatable conclusion that mathematical theories are, strictly speaking, not true. But fictionalists don’t deny that they serve their purposes in corresponding discourses. In other words, they say that mathematics is colloquially true, but not literally true, since mathematical objects don’t exist. The debate is far from being over, and there is even no clear favorite. If you’re interested in the arguments of both sides, I suggest you read this entry.

Propositions

I’ve already covered what propositions are in my post about Truth, so here is a short recap. There are sentences describing mental attitudes. They represent the same pattern: A [believes OR thinks OR desires OR etc.] that P, where P is a proposition.

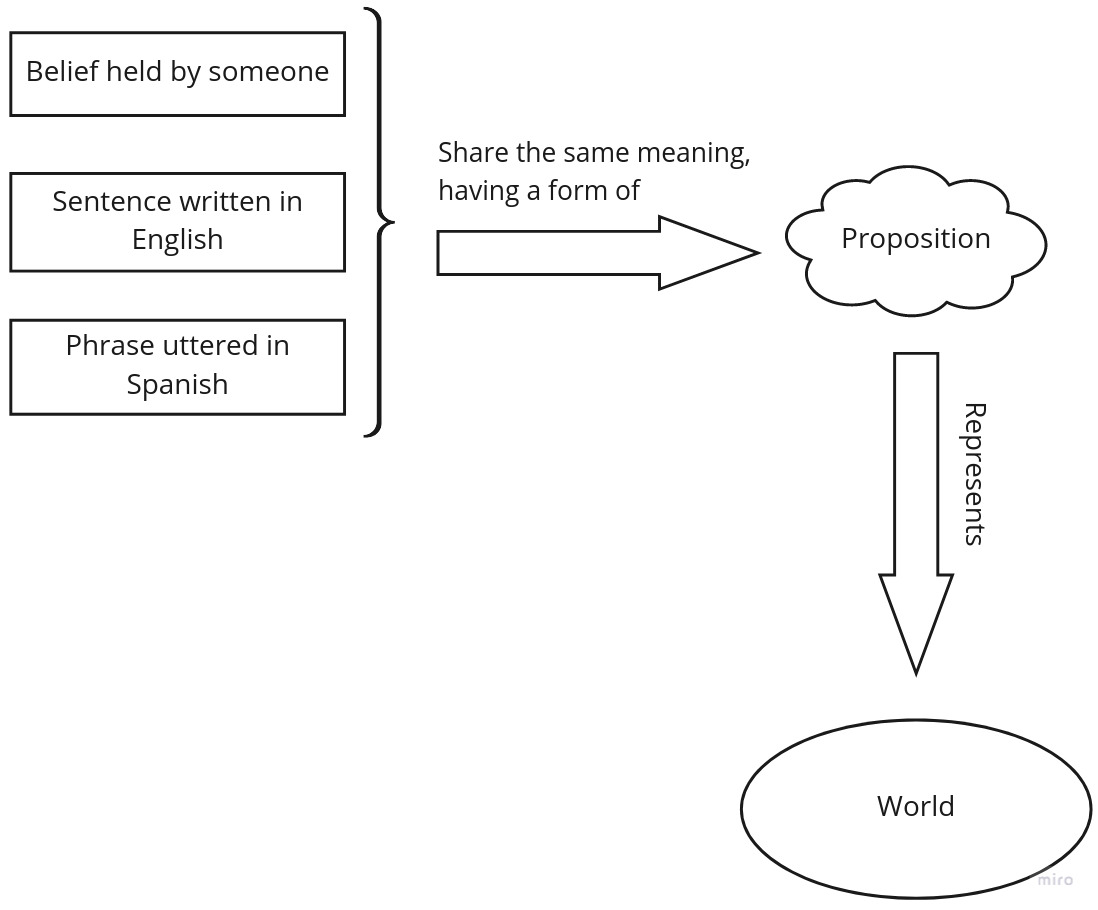
The general argument about whether propositions are abstract or not largely mirrors the one regarding numbers.

Since a proposition represents a singular term, what kind of entity does that term refer to? Can it refer to some mental entity? It’s unlikely because two distinct human beings speaking different languages can believe the same thing. But what is that single thing like?

It’s even more unlikely that propositions could refer to some physical objects. Lots of them have never been tokenized in any way, that is, they’ve never been written down, or painted, or vocalized. On the other hand, lots of them have billions of tokens, all in different languages and dated to different times. Which one is the token that represents a proposition?

Fictional Nominalists are in a relatively good position here. Just like with numbers, they claim that all sentences like “A [believes OR thinks OR desires OR etc.] that P” are, strictly speaking, false, because Ps are supposed to refer to propositions, but propositions, being abstract objects, don’t exist. But nevertheless, fictionalists admit that colloquially speaking, they can truthfully reflect mental attitudes of their bearers.

Finally, if we’re OK with admitting abstract objects’ existence, the thing that different people’s mental entities refer to is exactly it - a proposition, and it is an abstract object.

Further development of the Way of Negation

The way of negation was elaborated further. It’s divided into two main criteria taking two different (not very much so, actually) views at the problem. Those perspectives cover non-spatiality and causal inefficacy.

The non-spatiality criterion

We can start with an understanding of abstract objects as simple as being non-spatial. Where was the cosine function last Thursday after all? This question doesn’t seem to make much sense. A good example is mathematical entities. They are canonical abstract objects (at least in Platonists’ camp), and they vividly illustrate the point. Cosine function has neither spatial nor temporal properties. So does number seven. In contrast, a cosine function plot I’ve just drawn on my office board with a marker is concrete enough. I can say where it is and how much space it occupies. Moreover, I can say where it is at any given moment of time. If tomorrow someone moves the board, I’ll be able to say that my plot is in another room. And here is the question that helps to mark an abstract-concrete distinction in light of this example: “Where it is now and how much space does it occupy?” In case there is no sensible answer to this question, an object is abstract.

The causal inefficacy criterion

As the heading goes, an object is abstract if it is causally inefficacious. First of all, the cause-and-effect relation is understood as a physical interaction. In other words, causality implies physical contact. Thus, by the current delineation, abstract objects can’t have it. Number seven makes nothing happen, as well as Monday, architecture, red color, or Matt Berninger’s latest album. This account echoes with the previous section on spatiality: non-spatial objects apparently can’t have physical contact.

According to this account, mental objects such as thoughts can be considered to be concrete. Well, at least they can be viewed as not abstract. First of all, our thoughts are just a unique combination of fired neurons, and neurons are physical. Second, they can make us actually do something by means of physical interaction with each other. For instance, wintertime in and of itself doesn’t make me buy tickets in Thailand for vacation; it’s my perception of short daylight and cold weather that does.

Example: Properties as Abstract Objects

Let’s assume that we’ve already gone through defending our Realistic (and most probably, Platonistic) views on properties and arrived at the conclusion that properties are abstract entities (if not, check out this section). So, properties are non-mental (contrary to Conceptualism), non-physical and non-spatial (contrary to Immanent Realism), causally inefficacious (contrary to Trope Nominalism, where you view properties as tropes, and tropes are objects - incomplete ones, but causally-efficacious objects nevertheless), and they exist (contrary to Fictional Nominalism and Predicate Nominalism, where there are red apples, but no distinct thing representing red property). We can call them abstract entities. In order for them to become abstract objects, they should pass through two stages.

Nominalization

First, properties must be nominalized. This process has a theoretical foundation (it’s behind an additional paywall even if you already have a paid access to jstor) which is quite hard to tear through, but overall it’s quite intuitive anyway. All you have to do is asking “What is it?”-kind of questions. Being warm turns to temperature, being 74 meters turns to height.

A useful concept that can be employed here is determinable and determinate properties. The relation between them is akin to a genus-species or type-token ones. In other words, a determinate property is a special and concrete case of a determinable one. And the set of all determinate properties forms a determinable property.

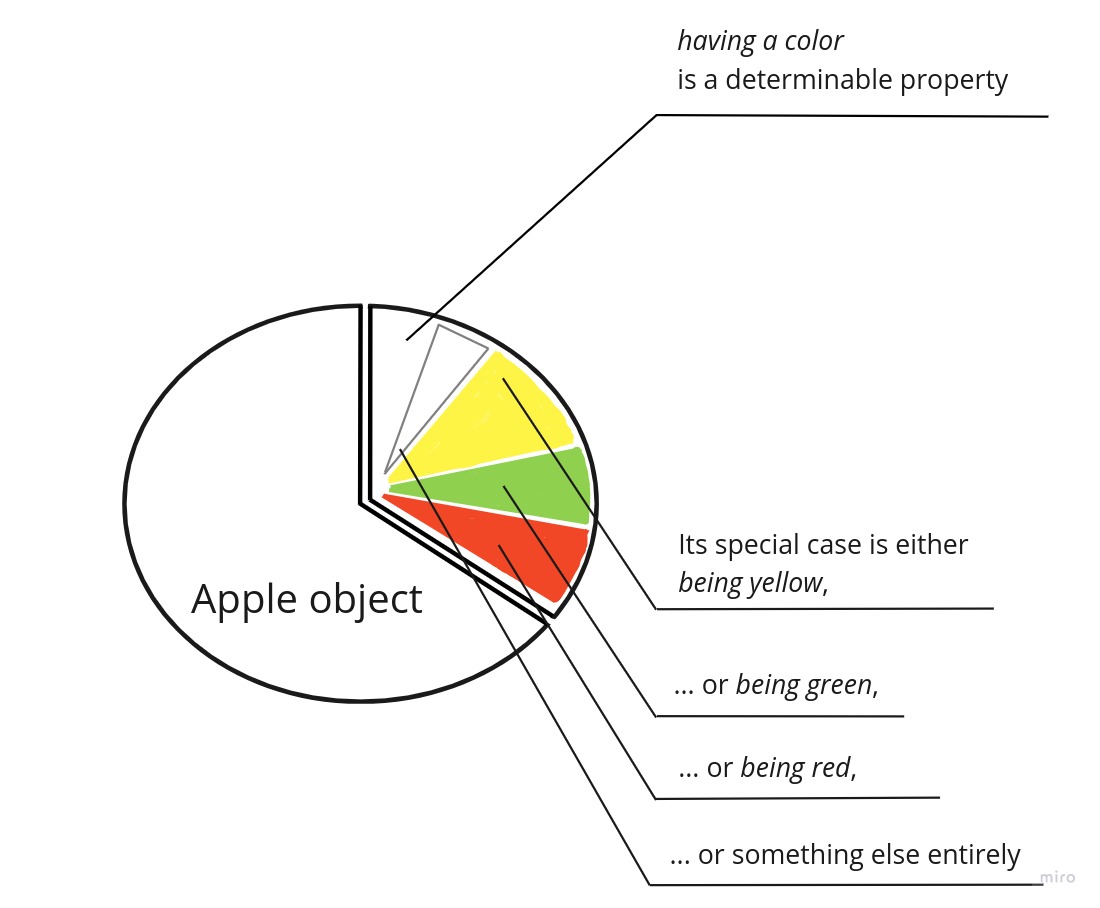
For example, being red is a special case of being colored, or, having a color. And being red, along with being black, being blue, etc, forms the property of being colored. That’s why we can say that being red is being colored. Or, red is a color. In this case, color is a higher-level type, or kind. So while I might struggle at first to nominalize being 74 meters, I ask myself what’s its determinable property, realize that depending on a context it could be for instance having a height, and after that end up with a height-type. Thus, the property of being 74 meters turns into an object 74 meters, which belongs to a height-type. Just in the same way, I can ask what is the determinable property of being warm. If I’m struggling to do that, I can name the properties residing on the same abstraction level. Those properties are incompatible with each other, that is, they can’t be obtained by a single object at the same time. For being warm, some of the neighboring properties are being hot and being cold. Thus, I can conclude that all of them are determinate properties of having a temperature property that can easily be turned into a temperature-kind embracing more specific objects like warm-temperature, hot-temperature, and cold-temperature.

Aristotle’s categories can help sometimes. Nine of ten of them are the things said of a primary substance. They are general and higher-level indeed but nevertheless can give some clue at hard times.

Identity

Second, the resulting abstract entity must have an identity. In other words, you should have the facility to tell the difference between abstract entities of the same kind. For example, being blue can be nominalized to a blue color. What is its identity? How is it different from a red color? The answer is a specific wavelength that any given color has. That’s what makes the blue color blue. That’s what makes it different from the red color.

Immutability

Abstract objects derived this way are inherently immutable. Blue color can’t become red color, but my neighbor’s car color can. Determinate colors can change each other within their corresponding determinable property so that color can change from red to blue. Ditto, the temperature can change from high to low, but the high temperature remains itself forever.

Fictional characters

They have an identity, like Sherlock Holmes, they are not physical, since he exists only as a fictional character, he once was mental - when his details and traits were thought out by Arthur Conan Doyle - but now even if no one is thinking of Mr. Holmes at some moment of time, he still exists. Besides, he’s both causally inefficacious and exists out of space (and starting from the creation, out of time). So fictional characters can be viewed as abstract objects either.

The Way of Abstraction

This is the second mainstream way of defining an abstract object.

Abstraction process

In a nutshell, an abstraction process is a mental process that goes like this. You consider several similar objects, pile off non-essential properties that distinguish them, and leave only essential ones shared by all of the objects. For example, I’ve seen a lot of apples in my life. What properties are mutual to all of them? Well, in my experience, they all have quite a narrow range of size, mass, their shape is similar either, and they are mostly green, yellow, or red. Thus, at a certain point in my life, when I had been seeing enough apples, I arrived at the abstract idea of what it is to be an apple. But this idea, or concept, is a mental entity inherent to my mind. Luckily, there are other people whose life experiences made them draw the same conclusion about apples. That’s why when we apple-lovers gather and talk about apples, we mean the same thing. And that thing, a referent of all our ideas about apples, is widely considered to be an abstract object representing an apple-kind.

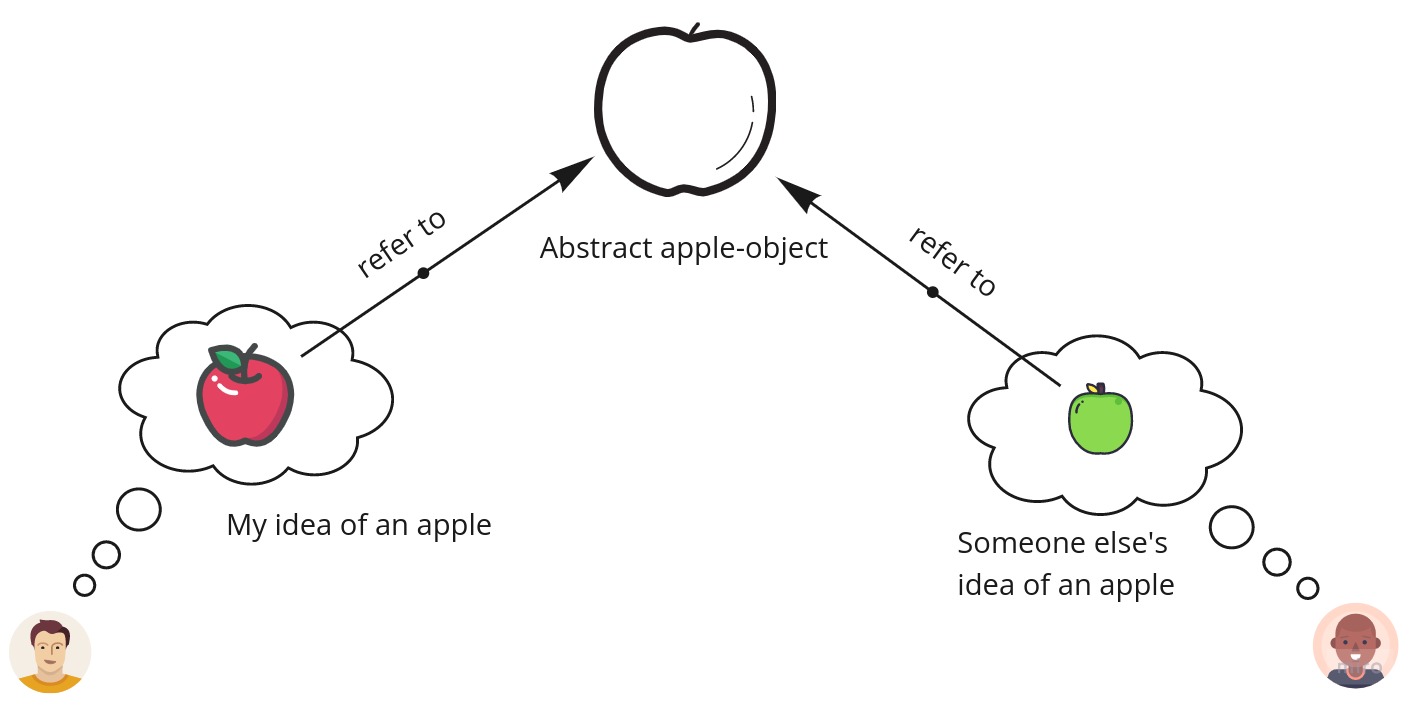
Just as a side note, the result of an abstraction process can be a determinable property. The processes of abstraction and property nominalization are inherently the same indeed: both involve either an abstraction discovery or abstraction creation. Looking at the creative side, I bet it took a lot of time for mankind to discover an apple abstraction so that anyone could easily say “Oh, that’s an apple” when having been shown an apple. Ditto, when a two-year-old sees a green cucumber and red apple, she might not immediately come up with a concept of color, especially if she hasn’t thought about that before. This process takes time. But adults don’t have to create too many abstractions these days. Most of them are already known, and the challenge is to discover them.
The place where you can have the most fun doing this is software development.

Equivalence relation nominalization with functional expressions

The term “functional expression” came from First-order logic. It’s what you might already know from mathematics as a Boolean-valued function: it’s a function taking some entity or entities as input and returning a Boolean value - True or False.

In the Philosophy of Language, a good example of a functional expression is a predicate. It takes the form of P(x), where P is a predicate, and x is a specific object that predicate P holds a truth value about. For example, take the sentence “This apple is red”. It has a predicate “is red” and a subject “this apple”. We can construct a functional expression IsRed denoting a predicate “is red”. It takes different objects as arguments. Let’s denote an object referred to earlier by a proper noun “this apple” as a. Thus, IsRed(a) is true. If I denote “my keyboard” in “My keyboard is black” as k, IsRed(k) is false.

Another example of functional expressions is a linguistic construct of the form “x of y”, for example, “a shape of an apple”, “a color of an apple”, etc. Many objects that we consider abstract are formed by means of functional expressions of this kind. It’s not always the case though, for instance, “the teacher of Aristotle” denotes Plato, and he was a concrete object. Here is an equation that helps to distinct abstract objects from concrete ones:

f(a) = f(b) iff Rab, where f(x) is a functional expression, and R is an equivalence expression.

In plain English, it means that there is an abstract object formed with f only if there is some equivalence relation between objects that functional expression f is applied to. For example, a color of an apple a equals a color of an apple b if the wavelength of light they reflect is the same. Here, “a color of an apple” is a functional expression, and “the wavelength of light they reflect is the same” is an equivalence relation. Another example: a direction of line a equals a direction of line b iff a is parallel to b.

The key point here is that equivalence relation is often epistemologically prior to corresponding abstract objects denoted by proper nouns. In this section, I’m interested in ways to come up with abstract objects, so the former is of particular importance. For instance, one might say that we wouldn’t have had a concept of direction unless there were no objects pointing the same way. In this case, we can say that the concept of parallel lines is epistemologically prior to the concept of direction; in other words, in some cases, first we learn about an equivalence relation, and then we construct knowledge of an abstract object. Just the same way, the concept of a wavelength is epistemologically prior to the concept of color: specific wavelength both describes and justifies the resulting color; it’s akin to a definition of what a color is from a dictionary.

Just to reiterate, parallel lines turn into a direction, and light reflected with the same wavelength turns into color. To put it another way, an abstract object is a result of an equivalence relation nominalization. Once again, this account of abstract objects holds true only for those ones that are expressed by means of a functional expression outlined above and reinforced with an equivalence relation. It doesn’t have an immediately clear application for Monday, anger, the proposition expressed with my desire to have some filter coffee, or number seven. So it’s not a necessary condition that abstract objects must hold.

Nominalization of other kinds of relations

I’ve briefly covered relations in general in my post on Properties, with intentional stress on resemblance relations. Short recap. Relation, unlike property, implies that there are more than one objects taking part in it. In other words, relations hold between things, in contrast to properties which hold of the things that possess them. There are two kinds of relations: internal and external. Internal relations are those that hold in virtue of their relata. Another way of saying this is that internal relation holds in virtue of the intrinsic properties of objects it relates. This definition draws the following question: which properties are intrinsic, and which are not? A common way to reply to this is that intrinsic properties hold because of the way an object is, and extrinsic ones do in virtue of other objects. For example, having a mass is widely considered to be an intrinsic property, in contrast to having a weight, which is obtained in virtue of other objects. Thus, is more massive than is an internal relation, while having greater weight than is an external one. It’s a matter of ongoing debates whether relations find their place under the sun in the metaphysical ontology; and if they do, it’s still a matter of further debates which ones are intrinsic and which ones are extrinsic. Relational properties, on the contrary, are largely accepted in the metaphysical community. They play a key role in coming up with nominalized relations if you struggle to do it intuitively. Thus, the first step towards relations’ nominalization is turning it into a relational property.

Generally, it takes the following form. If there is a relation R between some object x and some object y, then each x has a relational property of holding R to a specific corresponding y or set of specific ys. Even if you don’t accept relations to be a part of metaphysical ontology, you can spot them in sentences as a consistent pattern of repetition in the world around you. I’ve already given some examples; for instance, they can take the following forms: “x has a greater weight than y”, or “x loves y”, or “x stands between y and z”. The patterns of repetition here are what we can call a relation even without an ontological commitment; here they are: has a greater weight than, loves, stands between. To turn relations into relational properties, you first need to bind an object denoted by a placeholder y to a specific value. In other words, this value gets somewhat frozen into relation. Now, instead of relation R, we have a property of Rx. For instance, a relation has a greater weight than turns into a property of having greater weight than Earth. Here is another example. Consider a relation is to the south-east of. Here is a corresponding linguistic pattern: “x is to the south-east of y”. Then, bind y to some specific value. For instance, the result might look like “x is to the south-east of New York”. Thus, I’ve ended up with an x’s property of being to the south-east of New York.

You’re already familiar with the next step: you should nominalize a resulting property with strategies outlined above, in the section about property nominalization. What is the determinable property of being to the south-east of New-York? No immediately clear answer? OK, what are the neighboring properties? Being to the north-east of Mexico, being to the north-west of Hawaii, etc. What embraces all of those properties? What do they all indicate? Probably it has something to do with location. But aren’t they too vague for location? It seems more like a cardinal direction, since there are quite a few objects to the north-west of Hawaii or to the south-east of New-York. So I can end up with a direction kind, which is an abstract object corresponding to a determinable property of being directed. Adverbs like south-east of New York, north-east of London, etc., all denote abstract objects falling under a direction kind; we can say that they are directions. Just in the same way, being to the south-west of New York and being to the north-east of London are determinate properties of being directed. Now we need to turn our attention to the question of identity. What identifies direction? What makes two directions equal? It depends on the context you operate in. On one hand, we can say that there are south directions, and they all are equal. On the other, we might be interested that all directions we regard as equal should lie on the same line; for instance, the south of Berlin equals the south of Prague; but doesn’t equal the south of Rome. And in the most strict sense, we might want the starting point of all equal directions to be the same.

Example: kinds as Abstract Objects

As I’ve mentioned earlier, carrying out an abstraction process, we arrive at an abstract object. For example, there are tons of concrete apples, but they all belong to a single kind. The easiest way to illustrate this is to consequently take all existing apples and ask “What is this?” The answer would be always the same  –  ”That is an apple”. Another way of saying that is “This thing belongs to an apple-kind”. Indeed, an abstraction process by the very definition results into emerging of a canonical entity possessing only features essential to all the specific instances; they are the properties that make all the concrete objects to be that object, or, more precisely, to belong to that kind.

Thus, any kind, being a result of an abstraction process, is an abstract object.

Current view of Metaphysical Ontology

For now, we know there are objects that can be either concrete or abstract; there are properties which can be viewed as abstract objects; and there are kinds, which can be viewed as abstract objects either.

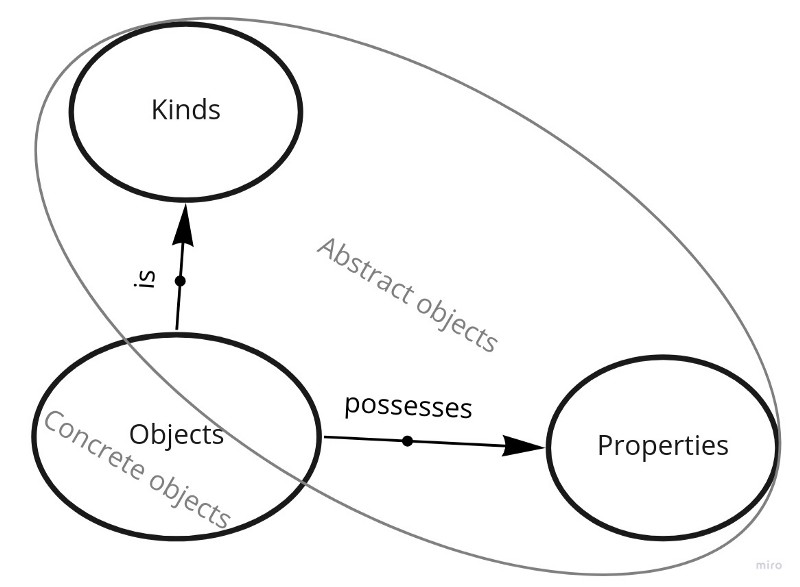
In the next post, we’ll take a closer look at kinds.

Further Reading

First of all, abstract objects entry on sep is classics. An interesting case of what can be viewed as an abstract object is color, and sep has a distinct entry for that.

I’ve given an inline link to sep platonism entry in this post a couple of times already, but it’s so great that I’d love to mention it one more time - -  please enjoy.

Fictionalism is a rival view on non-material, causally inefficacious objects, and it has gained significant attention lately. One prominent area where the rivalry is particularly interesting is the philosophy of mathematics, and no wonder both mathematical platonism and mathematical fictionalism have their place on sep.